(本小题满分12分)如图,平面直角坐标系中,抛物线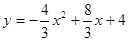 交
交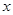 轴于A、B两点(点B在点A的右侧),交
轴于A、B两点(点B在点A的右侧),交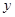 轴于点C,以OC、OB为两边作矩形OBDC,CD交抛物线于G.
轴于点C,以OC、OB为两边作矩形OBDC,CD交抛物线于G.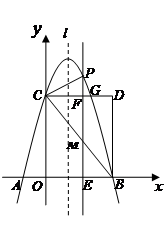
(1)求OC和OB的长;
(2)抛物线的对称轴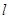 在边OB(不包括O、B两点)上作平行移动,交
在边OB(不包括O、B两点)上作平行移动,交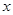 轴于点E,交CD于点F,交BC于点M,交抛物线于点P.设OE=m,PM=h,求h与m的函数关系式,并求出PM的最大值;
轴于点E,交CD于点F,交BC于点M,交抛物线于点P.设OE=m,PM=h,求h与m的函数关系式,并求出PM的最大值;
(3)在(2)的情况下,连接PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△BEM相似?若存在,直接写出此时m的值,并直接判断此时△PCM的形状;若不存在,请说明理由.
相关知识点
推荐套卷

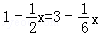 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号