为推广阳光体育“大课间”活动，我市某中学决定在学生中开设A：实心球，B：立定跳远，C：跳绳，D：跑步四种活动项目。为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调査结果绘制成如图①、②的统计图．请结合图中的信息解答下列问题：

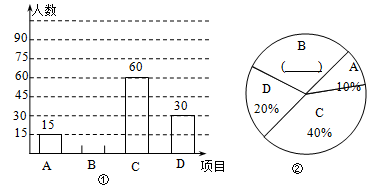
（1）在这项调査中，共调査了多少名学生？
（2）请将两个统计图补充完整；
（3）若调査到喜欢“跳绳”的5名学生中有3名男，2名女生．现从这5名学生中任意抽取2名学生，请用画树状图或列表的方法，求出刚好抽到同性别学生的概率．

A 10%