如图，平行四边形 ABCD对角线交于点O，点E是线段BO上的动点（与点B､O不重合），连接CE，过A点作AF∥CE交BD于点F，连接AE与CF．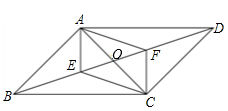
（1）求证：四边形AECF是平行四边形；
（2）当BA=BC=2，∠ABC=60°时，平行四边形 AECF能否成为正方形?若能，求出BE的长；若不能，请说明理由．
，
，
，求AB的长．
，求代数式
的值．
时，求代数式
的值．相关知识点
推荐套卷
如图，平行四边形 ABCD对角线交于点O，点E是线段BO上的动点（与点B､O不重合），连接CE，过A点作AF∥CE交BD于点F，连接AE与CF．
（1）求证：四边形AECF是平行四边形；
（2）当BA=BC=2，∠ABC=60°时，平行四边形 AECF能否成为正方形?若能，求出BE的长；若不能，请说明理由．
粤公网安备 44130202000953号