某学校游戏节活动中,设计了一个有奖转盘游戏,如图,A转盘被分成三个面积相等的扇形,B转盘被分成四个面积相等的扇形,每一个扇形都标有相应的数字,先转动A转盘,记下指针所指区域内的数字,再转动B转盘,记下指针所指区域内的数字(当指针在边界线上时,重新转动一次,直到指针指向一个区域内为止),然后,将两次记录的数据相乘.
(1)请利用画树状图或列表的方法,求出乘积为负数的概率;
(2)如果乘积是无理数时获得一等奖,那么获得一等奖的概率是多少?
相关知识点
推荐套卷
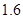 倍.小明购买火车票时发现,乘坐动车组比乘坐特快列车少用6小时.求小明乘坐动车组到上海需要的时间.
倍.小明购买火车票时发现,乘坐动车组比乘坐特快列车少用6小时.求小明乘坐动车组到上海需要的时间.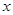 的一元二次方程
的一元二次方程 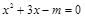 有实数根.
有实数根. 的取值范围
的取值范围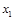 和
和 ,且
,且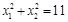 求
求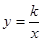 (x>0)交于点A(3,m),与x轴交于点B.
(x>0)交于点A(3,m),与x轴交于点B.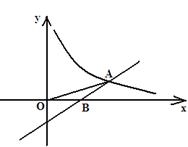
 中,
中, 的角平分线
的角平分线 交
交 边于
边于 .以
.以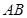 边上一点
边上一点 为圆心,过
为圆心,过 两点作
两点作 (不写作法,保留作图痕迹),再判断直线
(不写作法,保留作图痕迹),再判断直线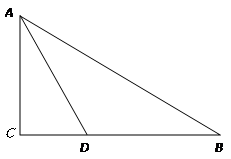
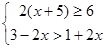 并把它的解集表示在数轴上.
并把它的解集表示在数轴上. 粤公网安备 44130202000953号
粤公网安备 44130202000953号