本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
某油库的设计容量为30万吨,年初储量为10万吨,从年初起计划每月购进石油 万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前
万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前 个月的需求量
个月的需求量 (万吨)与
(万吨)与 的函数关系为
的函数关系为 ,并且前4个月,区域外的需求量为20万吨.
,并且前4个月,区域外的需求量为20万吨.
(1)试写出第 个月石油调出后,油库内储油量
个月石油调出后,油库内储油量 (万吨)与
(万吨)与 的函数关系式;
的函数关系式;
(2)要使16个月内每月按计划购进石油之后,油库总能满足区域内和区域外的需求,且每月石油调出后,油库的石油剩余量不超过油库的容量,试确定 的取值范围.
的取值范围.
推荐套卷
 若
若 ,且
,且 。求
。求
 ,
, .
. ,求函数
,求函数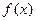 关于
关于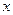 的解析式;
的解析式; ,
, ,函数
,函数 .
. 的最大值及相应的
的最大值及相应的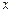 的值;(Ⅱ)若
的值;(Ⅱ)若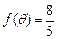 ,求
,求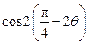 的值.
的值. 的定义域(要求用区间表示)。
的定义域(要求用区间表示)。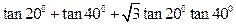 的值,
的值, 粤公网安备 44130202000953号
粤公网安备 44130202000953号