（本小题满分12分）
下面的一组图形为某一四棱锥S-ABCD的侧面与底面。
 |
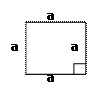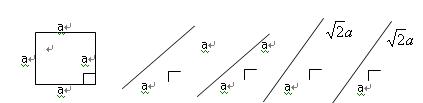
（1）请画出四棱锥S-ABCD的示意图，是否存在一条侧棱垂直于底面？如果存在，请给出证明；如果不存在，请说明理由
（2）若SA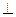
面ABCD，E为AB中点，求二面角E-SC-D的大小
（3）求点D到面SEC的距离
相关试题
·z+2i
.
；
+
.
+(
+3sin
+(m2+2m-3)i,当m为何值时，（1）z∈R；（2）z是纯虚数；（3）z对应的点位于复平面第二象限；（4）z对应的点在直线x+y+3=0上.推荐套卷
（本小题满分12分）
下面的一组图形为某一四棱锥S-ABCD的侧面与底面。
|
（1）请画出四棱锥S-ABCD的示意图，是否存在一条侧棱垂直于底面？如果存在，请给出证明；如果不存在，请说明理由
（2）若SA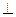面ABCD，E为AB中点，求二面角E-SC-D的大小
（3）求点D到面SEC的距离
粤公网安备 44130202000953号