(本小题满分16分)若数列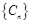 满足①
满足①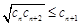 ,②存在常数
,②存在常数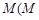 与
与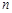 无关),使
无关),使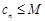 .则称数列
.则称数列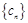 是“和谐数列”.
是“和谐数列”.
(1)设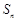 为等比数列
为等比数列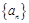 的前
的前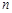 项和,且
项和,且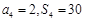 ,求证:数列
,求证:数列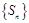 是“和谐数列”;
是“和谐数列”;
(2)设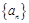 是各项为正数,公比为q的等比数列,
是各项为正数,公比为q的等比数列,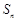 是
是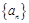 的前
的前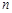 项和,求证:数列
项和,求证:数列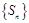 是“和谐数列”的充要条件为
是“和谐数列”的充要条件为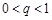 .
.
推荐套卷
(本小题满分16分)若数列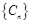 满足①
满足①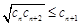 ,②存在常数
,②存在常数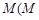 与
与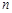 无关),使
无关),使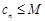 .则称数列
.则称数列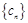 是“和谐数列”.
是“和谐数列”.
(1)设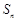 为等比数列
为等比数列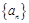 的前
的前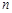 项和,且
项和,且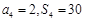 ,求证:数列
,求证:数列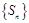 是“和谐数列”;
是“和谐数列”;
(2)设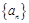 是各项为正数,公比为q的等比数列,
是各项为正数,公比为q的等比数列,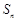 是
是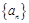 的前
的前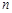 项和,求证:数列
项和,求证:数列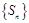 是“和谐数列”的充要条件为
是“和谐数列”的充要条件为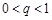 .
.