已知抛物线
顶点为O（0,0）,焦点为F（1,0）,A为C上异于顶点的任意一点，过点A的直线
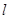交C 于另一点B,交x轴的正半轴于点D,且有
，延长AF交曲线C于点E.过点E作直线
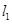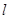平行于, 设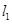与此抛物线准线交于点
.
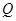（Ⅰ）求抛物线的的方程；
（Ⅱ）设点
的纵坐标分别为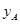
、
、
，求
的值；
（Ⅲ）求
面积的最小值.
相关试题
满足：
，且
成等比数列．
；
对任意
恒成立，试猜想出实数
的最小值，并证明．
．
在区间
上的最大值；
在区间
上存在递减区间，求实数m的取值范围．
，且
．
的值； 
的值．
中，
，且前
项的算术平均数等于第
倍（
）。
,且当
及
时取得极值。
的解析式；
与
有两个不同的交点，求实数
的取值范围.相关知识点
推荐套卷
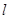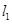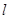已知抛物线顶点为O（0,0）,焦点为F（1,0）,A为C上异于顶点的任意一点，过点A的直线交C 于另一点B,交x轴的正半轴于点D,且有，延长AF交曲线C于点E.过点E作直线平行于, 设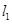与此抛物线准线交于点.
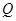（Ⅰ）求抛物线的的方程；
（Ⅱ）设点的纵坐标分别为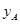、、，求的值；
（Ⅲ）求面积的最小值.
粤公网安备 44130202000953号