如图,在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm,点P、Q同时从点C出发,分别沿C→A和 C→B的方向运动,速度分别为2cm/s和1cm/s.过点P作PM⊥AC交AB于M,分别连接PQ、PM.当点Q运动到B时,两点都停止.设运动时间为t秒.
(1)当t= s时,PQ⊥QM?
(2)将△PQM沿PM翻折,得到△PMQ/.
①当t= s时,点Q/恰好落在AB上;
②设△PMQ/与△ABC重叠部分的面积为Scm2,求:S与t的函数关系式,并指出t的取值范围.
相关知识点
推荐套卷
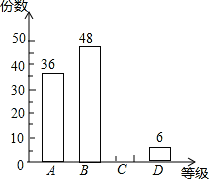
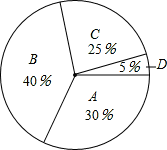
 |=0
|=0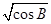 -(3+tanC)0的值.
-(3+tanC)0的值. ,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号