如图,一个粒子在第一象限内及x轴,y轴上运动,第一分钟内从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),而后它接着按图中箭头所示的与x轴,y轴平行的方向来回运动,且每分钟移动1个长度单位。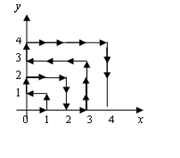
(1)当粒子所在位置是(2,2)时,所经过的时间是 ;
(2)在第2014分钟时,这个粒子所在位置的坐标是 。
相关知识点
推荐套卷
如图,一个粒子在第一象限内及x轴,y轴上运动,第一分钟内从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),而后它接着按图中箭头所示的与x轴,y轴平行的方向来回运动,且每分钟移动1个长度单位。
(1)当粒子所在位置是(2,2)时,所经过的时间是 ;
(2)在第2014分钟时,这个粒子所在位置的坐标是 。