(本小题满分14分)如图,某城市有一条公路从正西方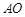 通过市中心
通过市中心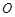 后转向东偏北
后转向东偏北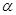 角方向的
角方向的 .位于该市的某大学
.位于该市的某大学 与市中心
与市中心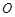 的距离
的距离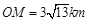 ,且
,且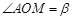 .现要修筑一条铁路L,L在OA上设一站
.现要修筑一条铁路L,L在OA上设一站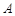 ,在OB上设一站B,铁路在
,在OB上设一站B,铁路在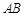 部分为直线段,且经过大学
部分为直线段,且经过大学 .其中
.其中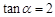 ,
,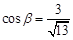 ,
,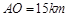 .
.
(1)求大学 与站
与站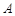 的距离
的距离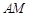 ;
;
(2)求铁路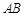 段的长
段的长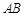 .
.
推荐套卷
(本小题满分14分)如图,某城市有一条公路从正西方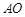 通过市中心
通过市中心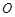 后转向东偏北
后转向东偏北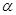 角方向的
角方向的 .位于该市的某大学
.位于该市的某大学 与市中心
与市中心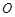 的距离
的距离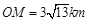 ,且
,且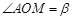 .现要修筑一条铁路L,L在OA上设一站
.现要修筑一条铁路L,L在OA上设一站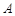 ,在OB上设一站B,铁路在
,在OB上设一站B,铁路在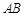 部分为直线段,且经过大学
部分为直线段,且经过大学 .其中
.其中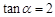 ,
,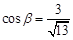 ,
,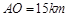 .
.
(1)求大学 与站
与站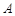 的距离
的距离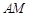 ;
;
(2)求铁路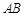 段的长
段的长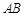 .
.