（本小题满分12分）最新高考改革方案已在上海和江苏开始实施，某教育机构为了解我省广大师生对新高考改革方案的看法，对某市部分学校500名师生进行调查，统计结果如下：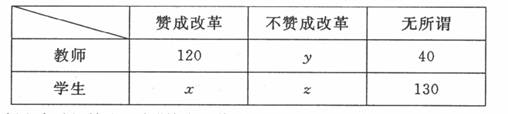
在全体师生中随机抽取1名“赞成改革”的人是学生的概率为0.3，且x=2y.
（Ⅰ）现从全部500名师生中用分层抽样的方法抽取50名进行问卷调查，则应抽取“不
赞成改革”的教师和学生人数各是多少？
（Ⅱ）在（Ⅰ）中所抽取的“不赞成改革”的人中，随机选出三人进行座谈，求至少有一名
教师被选出的概率。
相关试题
函数
的值域为R； 
:不等式
，对
∈（-∞，-1）上恒成立，如果命题“
”为真命题，命题“
”为假命题，求实数
的取值范围．（本小题满分12分）已知关于
的二次函数
（Ⅰ）设集合
和
，分别从集合
，
中随机取一个数作为
和
，求函数
在区间
上是增函数的概率．
（Ⅱ）设点
是区域
内的随机点，求函数
在区间上是增函数的概率．
（本小题满分12分）某城市100户居民的月平均用电量（单位：度），以[160，180），[180，200），[200，200），[220．240），[240，260），[260，280），[280，300）分组的频率分布直方图如图．
（1）求月平均用电量的众数和中位数；
（2）在月平均用电量为[220．240），[240，260），[260，280），[280，300）的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在[240．260）的用户中应抽取多少户？
：
，（
不同时为0），
：
，
且
，求实数
的值；
且
时，求直线
，且
．
的解析式；
时，有
，求
的取值范围推荐套卷
粤公网安备 44130202000953号