(本小题满分12分)
某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为x(0<x<1),则出厂价相应提高的比例为0.7x,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(Ⅰ)若年销售量增加的比例为0.4x,为使本年度的年利润比上年度有所增加,则投入成本增加的比例x应在什么范围内?
(Ⅱ)年销售量关于x的函数为y=3240(-x2+2x+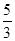 ),则当x为何值时,本年度的年利润最大?最大利润为多少?
),则当x为何值时,本年度的年利润最大?最大利润为多少?