已知函数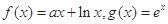 .
.
(I)当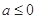 时,求
时,求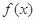 的单调区间
的单调区间
(Ⅱ)若不等式 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;
(Ⅲ)定义:对于函数 和
和 在其公共定义域内的任意实数
在其公共定义域内的任意实数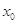 ,称
,称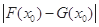 的值为两函数在
的值为两函数在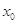 处的差值。证明:当
处的差值。证明:当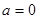 时,函数
时,函数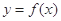 和
和 在其公共定义域内的所有差值都大干2。
在其公共定义域内的所有差值都大干2。
推荐套卷
已知函数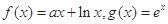 .
.
(I)当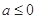 时,求
时,求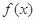 的单调区间
的单调区间
(Ⅱ)若不等式 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;
(Ⅲ)定义:对于函数 和
和 在其公共定义域内的任意实数
在其公共定义域内的任意实数 ,称
,称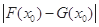 的值为两函数在
的值为两函数在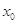 处的差值。证明:当
处的差值。证明:当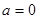 时,函数
时,函数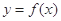 和
和 在其公共定义域内的所有差值都大干2。
在其公共定义域内的所有差值都大干2。