(本小题满分14分)已知椭圆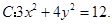
(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)设椭圆 上在第二象限的点
上在第二象限的点 的横坐标为
的横坐标为 ,过点
,过点 的直线
的直线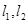 与椭圆
与椭圆 的另一交点分别为
的另一交点分别为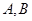 .且
.且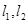 的斜率互为相反数,
的斜率互为相反数,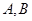 两点关于坐标原点
两点关于坐标原点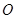 的对称点分别为
的对称点分别为 ,求四边形
,求四边形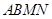 的面积的最大值.
的面积的最大值.
推荐套卷
(本小题满分14分)已知椭圆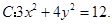
(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)设椭圆 上在第二象限的点
上在第二象限的点 的横坐标为
的横坐标为 ,过点
,过点 的直线
的直线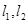 与椭圆
与椭圆 的另一交点分别为
的另一交点分别为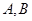 .且
.且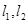 的斜率互为相反数,
的斜率互为相反数,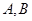 两点关于坐标原点
两点关于坐标原点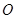 的对称点分别为
的对称点分别为 ,求四边形
,求四边形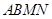 的面积的最大值.
的面积的最大值.