为了让学生了解党的十八大精神,某中学举行了一次“社会主义核心价值观暨八礼四仪知识竞赛”,共有1000名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频数分布表和频数分布直方图,解答下列问题:
(1)a= ,b= ;
(2)补全频数分布直方图;
(3)在该问题中的样本容量是多少? 答: .
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为 人?
相关知识点
推荐套卷
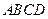 中,
中,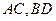 为对角线,将
为对角线,将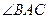 绕顶点
绕顶点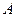 逆时针旋转
逆时针旋转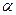 °(
°(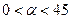 ),旋转后角的两边分别交
),旋转后角的两边分别交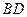 于点
于点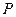 、点
、点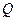 ,交
,交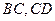 于点
于点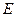 、点
、点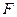 ,联结
,联结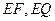 .
.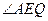 的大小是否改变,若不变写出它的度数,若改变,写出它的变化范围(直接在答题卡上写出结果,不必证明);
的大小是否改变,若不变写出它的度数,若改变,写出它的变化范围(直接在答题卡上写出结果,不必证明);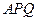 与△
与△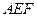 的面积的数量关系,写出结论并加以证明.
的面积的数量关系,写出结论并加以证明.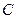 :
: 的顶点在坐标轴上.
的顶点在坐标轴上.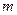 的值;
的值; 时,抛物线
时,抛物线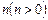 个单位后与抛物线
个单位后与抛物线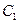 :
: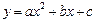 关于
关于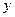 轴对称,且
轴对称,且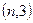 ,求
,求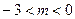 时,抛物线
时,抛物线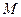 ,且过点
,且过点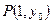 .问在直线
.问在直线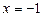 上是否存在一点
上是否存在一点 使得△
使得△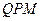 的周长最小,如果存在,求出点
的周长最小,如果存在,求出点 与正方形
与正方形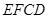 的位置如图所示.
的位置如图所示. 交
交 于点
于点 ;
;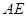 上取一点
上取一点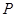 ,联结
,联结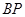 ,
,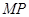 ,使△
,使△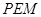 与△
与△ 相似;
相似; 是线段
是线段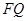 并延长交四边形
并延长交四边形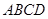 的一边于点
的一边于点 ,且满足
,且满足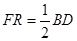 ,则
,则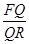 的值为_____________.
的值为_____________. 四种不同型号供顾客选择,它们每台的价格(单位:元)依次分别是:2500,4000,6000,10000.为做好下阶段的销售工作,商场调查了一周内这四种不同型号电视的销售情况,并根据销售情况,将所得的数据制成统计图,现已知该品牌一周内四种型号电视共售出240台,每台的销售利润占其价格的百分比如下表:
四种不同型号供顾客选择,它们每台的价格(单位:元)依次分别是:2500,4000,6000,10000.为做好下阶段的销售工作,商场调查了一周内这四种不同型号电视的销售情况,并根据销售情况,将所得的数据制成统计图,现已知该品牌一周内四种型号电视共售出240台,每台的销售利润占其价格的百分比如下表: 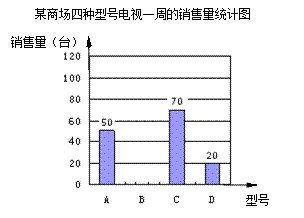
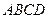 中,点
中,点 在对角线
在对角线 上,以
上,以 的长为半径的⊙
的长为半径的⊙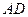 ,
,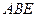 =∠
=∠ .
. 与⊙
与⊙
 ,
,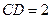 ,求⊙
,求⊙ 粤公网安备 44130202000953号
粤公网安备 44130202000953号