(本小题满分11分)已知关于x的函数y=m -x-(m-1).
-x-(m-1).
(1)m=__________时,y=m -x-(m-1)是一次函数;
-x-(m-1)是一次函数;
(2)求证:对任何实数m,y=m -x-(m-1)的图像与
-x-(m-1)的图像与 都有公共点;
都有公共点;
(3)若是关于 的二次函数y=m
的二次函数y=m -x-(m-1)的图像与x有两个不同的公共点A、B (点A在点B左边),图像顶点为C,且△ABC是等腰直角三角形,求m的值;
-x-(m-1)的图像与x有两个不同的公共点A、B (点A在点B左边),图像顶点为C,且△ABC是等腰直角三角形,求m的值;
(4)是否存在这样的点P,使得对任何实数m,y=m -x-(m-1)的图像都经过P点?若存在,求出所有P的坐标;若不存在,请说明理由.
-x-(m-1)的图像都经过P点?若存在,求出所有P的坐标;若不存在,请说明理由.
相关知识点
推荐套卷

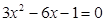 (配方法)(2)、
(配方法)(2)、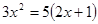 (公式法)
(公式法)
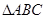 中,
中,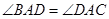 ,
,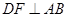 ,
, ,AF=10cm, AC=14cm,动点E以2cm/s的速度从
,AF=10cm, AC=14cm,动点E以2cm/s的速度从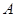 点向
点向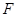 点运动,动点
点运动,动点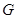 以1cm/s的速度从
以1cm/s的速度从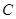 点向
点向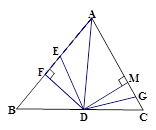
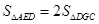 ;
;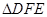 与
与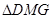 全等
全等 
 粤公网安备 44130202000953号
粤公网安备 44130202000953号