为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是: .
.
(1)求图中 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在 岁的
岁的
人数;
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场
的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要
负责人,记这3名志愿者中“年龄低于35岁”的人数为 ,求
,求 的分布列及
的分布列及
数学期望.
相关知识点
推荐套卷
 的函数
的函数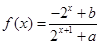 是奇函数.
是奇函数.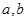 的值;
的值;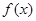 的单调性,并证明.
的单调性,并证明.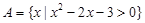 ,
, .
. ,使得
,使得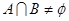 ,求
,求 的取值范围;
的取值范围;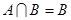 ,求
,求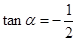 ,求
,求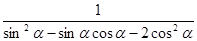 的值;
的值;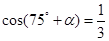 ,且
,且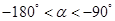 ,求
,求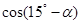 的值.
的值.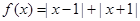 .
.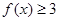 的解集;
的解集;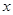 的不等式
的不等式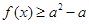 在
在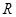 上恒成立,求实数
上恒成立,求实数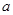 的取值范围.
的取值范围.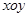 中,曲线
中,曲线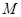 的参数方程为
的参数方程为 (
(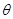 为参数),若以直角坐标系的原点
为参数),若以直角坐标系的原点 为极点,
为极点,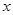 轴的正半轴为极轴建立极坐标,曲线
轴的正半轴为极轴建立极坐标,曲线 的极坐标方程为
的极坐标方程为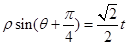 (其中
(其中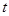 为常数).
为常数).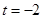 时,求曲线
时,求曲线 粤公网安备 44130202000953号
粤公网安备 44130202000953号