（本小题满分13分）从某企业生产的某种产品中抽取20件，测量这些产品的一项质量指标值，由测量得到如图的频率分布直方图，从左到右各组的频数依次记为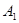
，
，
，
，
．
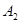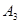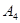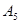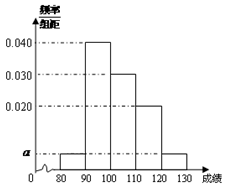
（1）求图中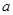
的值；
（2）下图是统计图中各组频数的一个算法流程图，求输出的结果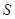
；
（3）从质量指标值分布在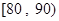
、
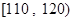的产品中随机抽取2件产品，求所抽取两件产品的质量指标值之差大于10的概率．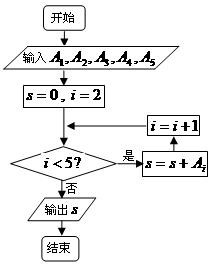
相关试题
不在同一平面内，求证：
既不平行也不相交．
的上、下两底边长之比为
，连接
，把正三棱台分成三个三棱锥，求这三个三棱锥的体积之比．
的棱长为
，它的四个互不相邻的顶点
，
，
，
构成一个正四面体的顶点，求这个正四面体的体积．
，
，
为三个平面，
，
．求证：
．
，如果
两两垂直且
，求这个球的体积．相关知识点
推荐套卷
（本小题满分13分）从某企业生产的某种产品中抽取20件，测量这些产品的一项质量指标值，由测量得到如图的频率分布直方图，从左到右各组的频数依次记为，，，，．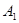
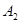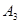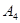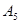（1）求图中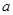的值；
（2）下图是统计图中各组频数的一个算法流程图，求输出的结果；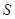
（3）从质量指标值分布在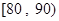、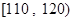的产品中随机抽取2件产品，求所抽取两件产品的质量指标值之差大于10的概率．
粤公网安备 44130202000953号