选修4—1:几何问题选讲
如图,已知AB是⊙O的直径,弦CD与AB垂直,垂足为M,E是CD延长线上的一点,且AB=10,CD=8,3DE=4OM,过F点作⊙O的切线EF,BF交CD于G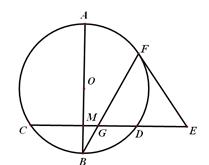
(Ⅰ)求EG的长;
(Ⅱ)连接FD,判断FD与AB是否平行,为什么?
推荐套卷
选修4—1:几何问题选讲
如图,已知AB是⊙O的直径,弦CD与AB垂直,垂足为M,E是CD延长线上的一点,且AB=10,CD=8,3DE=4OM,过F点作⊙O的切线EF,BF交CD于G
(Ⅰ)求EG的长;
(Ⅱ)连接FD,判断FD与AB是否平行,为什么?