(本小题满分12分)下图是某市今年1月份前30天空气质量指数(AQI)的趋势图.
(1)根据该图数据在答题卷中完成频率分布表,并在图中作出这些数据的频率分布直方图;

(图中纵坐标1/300即 ,以此类推)
,以此类推)
(2)当空气质量指数(AQI)小于100时,表示空气质量优良.某人随机选择当月1日至10日中的某一
天到达该市,并停留2天,设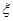 是此人停留期间空气质量优良的天数,求
是此人停留期间空气质量优良的天数,求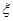 的数学期望.
的数学期望.
相关知识点
推荐套卷
(本小题满分12分)下图是某市今年1月份前30天空气质量指数(AQI)的趋势图.
(1)根据该图数据在答题卷中完成频率分布表,并在图中作出这些数据的频率分布直方图;

(图中纵坐标1/300即 ,以此类推)
,以此类推)
(2)当空气质量指数(AQI)小于100时,表示空气质量优良.某人随机选择当月1日至10日中的某一
天到达该市,并停留2天,设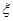 是此人停留期间空气质量优良的天数,求
是此人停留期间空气质量优良的天数,求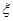 的数学期望.
的数学期望.