如图，某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树，已知角A为
的长度均大于200米，现在边界AP，AQ处建围墙，在PQ处围竹篱笆.
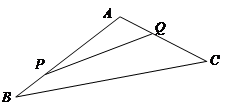
（1）若围墙AP，AQ总长度为200米，如何围可使得三角形地块APQ的面积最大？
（2）已知AP段围墙高1米，AQ段围墙高1.5米，造价均为每平方米100元.若围围墙用了20000元，问如何围可使竹篱笆用料最省？
的值
12分）在
中，角
对边分别为
，
面积为
，（1）求
的值（2）求
中，
，求
值
的值
中，已知
，
分别为等差数列
的第3项和第5项，试求数列
推荐套卷
如图，某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树，已知角A为的长度均大于200米，现在边界AP，AQ处建围墙，在PQ处围竹篱笆.
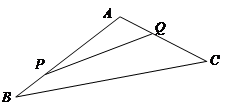
（1）若围墙AP，AQ总长度为200米，如何围可使得三角形地块APQ的面积最大？
（2）已知AP段围墙高1米，AQ段围墙高1.5米，造价均为每平方米100元.若围围墙用了20000元，问如何围可使竹篱笆用料最省？
粤公网安备 44130202000953号