如图，扇形OAB的半径OA=3，圆心角∠AOB=90°，点C是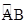
上异于A、B的动点，过点C作CD⊥OA于点D，作CE⊥OB于点E，连接DE，点G、H在线段DE上，且DG=GH=HE
（1）求证：四边形OGCH是平行四边形．
（2）当点C在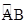上运动时，在CD、CG、DG中，是否存在长度不变的线段？若存在，请求出该线段的长度．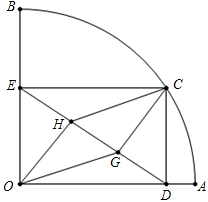
相关试题
如图，扇形OAB的半径OA=3，圆心角∠AOB=90°，点C是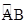上异于A、B的动点，过点C作CD⊥OA于点D，作CE⊥OB于点E，连接DE，点G、H在线段DE上，且DG=GH=HE
（1）求证：四边形OGCH是平行四边形．
（2）当点C在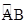上运动时，在CD、CG、DG中，是否存在长度不变的线段？若存在，请求出该线段的长度．
粤公网安备 44130202000953号