在平面直角坐标系中，一次函数y=ax+b的图象过点B（﹣1，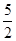
），与x轴交于点A（4，0），与y轴交于点C，与直线y=kx交于点P，且PO=PA，
（1）求a+b的值．
（2）求k的值．
（3）D为PC上一点，DF⊥x轴于点F，交OP于点E，若DE=2EF，求D点坐标．
在平面直角坐标系中，一次函数y=ax+b的图象过点B（﹣1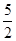，），与x轴交于点A（4，0），与y轴交于点C，与直线y=kx交于点P，且PO=PA，
（1）求a+b的值．
（2）求k的值．
（3）D为PC上一点，DF⊥x轴于点F，交OP于点E，若DE=2EF，求D点坐标．
－
, 求
的值.
,其中a =－8,b =
.
）2·（
）3÷（
xy）
÷
粤公网安备 44130202000953号