如图,在平面直角坐标系xOy中,一动直线l从y轴出发,以每秒1个单位长度的速度沿x轴向右平移,直线l与直线y=x相交于点P,以OP为半径的⊙P与x轴正半轴交于点A,与y轴正半轴交于点B.设直线l的运动时间为t秒.
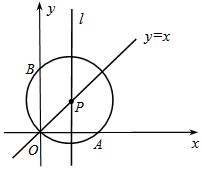
(1)填空:当t=1时,⊙P的半径为,OA=,OB=;
(2)若点C是坐标平面内一点,且以点O、P、C、B为顶点的四边形为平行四边形.
①请你直接写出所有符合条件的点C的坐标;(用含t的代数式表示)
②当点C在直线y=x上方时,过A、B、C三点的⊙Q与y轴的另一个交点为点D,连接DC、DA,试判断△DAC的形状,并说明理由.