给定一个数列
，在这个数列里，任取
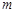
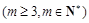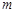项，并且不改变它们在数列中的先后次序，得到的数列的一个阶子数列.
已知数列的通项公式为
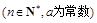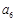，等差数列
，
，
是数列的一个3阶子数列.
（1）求
的值；
（2）等差数列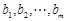
是的一个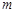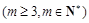阶子数列，且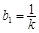
，求证：
；
（3）等比数列
是的一个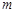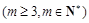阶子数列，求证：
.
相关试题
两个顶点
的坐标分别是
，边
所在直线的斜率之积等于
，求顶点
的轨迹方程，并画出草图。
的曲线是焦点在
上的椭圆 ，求
的取值范围
轴上，长轴长等于12，离心率等于
；椭圆经过点
；椭圆的一个焦点到长轴两端点的距离分别为10和4.
；（2）
；
；（4）
.
在点
处的切线与直线
垂直，求实数
的值.
，求
的最小值
；
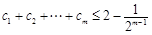.推荐套卷
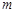
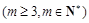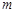给定一个数列，在这个数列里，任取项，并且不改变它们在数列中的先后次序，得到的数列的一个阶子数列.
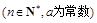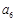已知数列的通项公式为，等差数列，，是数列的一个3阶子数列.
（1）求的值；
（2）等差数列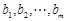是的一个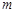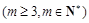阶子数列，且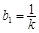，求证：；
（3）等比数列是的一个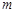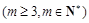阶子数列，求证：.
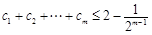粤公网安备 44130202000953号