（本小题满分12分）
已知函数f（x）＝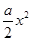
－bx＋lnx（a，b∈R）．
（Ⅰ）若a＝b＝1，求f（x）点（1，f（1））处的切线方程；
（Ⅱ）设a＜0，求f（x）的单调区间；
（Ⅲ）设a＜0，且对任意的x＞0，f（x）≤f（2），试比较ln（－a）与－2b的大小．
相关试题
＋
＝
；
－lg
＋lg12.5－log89·log278；
－log5
－log514；
×log3
×log5
.
×
0＋80.25×
＋(
×
)6－
；
；
推荐套卷
（本小题满分12分）
已知函数f（x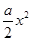）＝－bx＋lnx（a，b∈R）．
（Ⅰ）若a＝b＝1，求f（x）点（1，f（1））处的切线方程；
（Ⅱ）设a＜0，求f（x）的单调区间；
（Ⅲ）设a＜0，且对任意的x＞0，f（x）≤f（2），试比较ln（－a）与－2b的大小．
粤公网安备 44130202000953号