设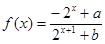 (
(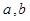 为实常数).
为实常数).
(1)当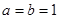 时,证明:
时,证明: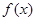 不是奇函数;
不是奇函数;
(2)设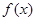 是奇函数,求
是奇函数,求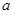 与
与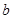 的值;
的值;
(3)当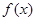 是奇函数时,研究是否存在这样的实数集的子集
是奇函数时,研究是否存在这样的实数集的子集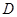 ,对任何属于
,对任何属于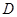 的
的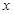 、c,都有
、c,都有 成立?若存在试找出所有这样的
成立?若存在试找出所有这样的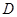 ;若不存在,请说明理由.
;若不存在,请说明理由.
推荐套卷
设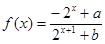 (
(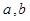 为实常数).
为实常数).
(1)当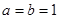 时,证明:
时,证明: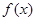 不是奇函数;
不是奇函数;
(2)设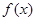 是奇函数,求
是奇函数,求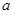 与
与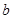 的值;
的值;
(3)当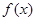 是奇函数时,研究是否存在这样的实数集的子集
是奇函数时,研究是否存在这样的实数集的子集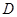 ,对任何属于
,对任何属于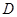 的
的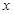 、c,都有
、c,都有 成立?若存在试找出所有这样的
成立?若存在试找出所有这样的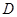 ;若不存在,请说明理由.
;若不存在,请说明理由.