(本小题满分16分)已知数列 、
、 ,其中,
,其中,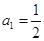 ,数列
,数列 的前
的前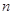 项和
项和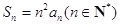 ,数列
,数列 满足
满足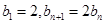 .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)是否存在自然数 ,使得对于任意
,使得对于任意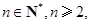 有
有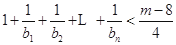 恒成立?若存在,求出
恒成立?若存在,求出 的最小值;
的最小值;
(3)若数列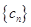 满足
满足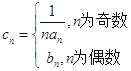 ,求数列
,求数列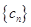 的前
的前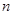 项和
项和 .
.
推荐套卷
(本小题满分16分)已知数列 、
、 ,其中,
,其中,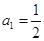 ,数列
,数列 的前
的前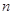 项和
项和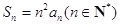 ,数列
,数列 满足
满足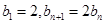 .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)是否存在自然数 ,使得对于任意
,使得对于任意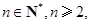 有
有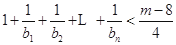 恒成立?若存在,求出
恒成立?若存在,求出 的最小值;
的最小值;
(3)若数列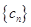 满足
满足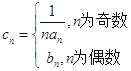 ,求数列
,求数列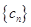 的前
的前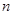 项和
项和 .
.