.已知圆C：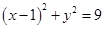
内有一点P（2，2），过点P作直线
l交圆C于A、B两点.
(1)当l经过圆心C时，求直线l的方程；
(2)当弦AB被点P平分时，写出直线l的方程；
(3) 当直线l的倾斜角为45º时，求弦AB的长.
相关试题
,
.
, 求
的值;
为坐标原点, 点
在第一象限, 求函数
的单调递增区间与值域.
中，
分别为角
的对边，
，
．
的值；
的值.
是等边三角形，
，
，
三点共线，
的值；
的长．
，且
，
的值;
的值
为数列
的前
项和，且
，
，
为等比数列；
，求数列
的前
；
，数列
的前
，求证：
．相关知识点
推荐套卷
.已知圆C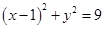：内有一点P（2，2），过点P作直线
l交圆C于A、B两点.
(1)当l经过圆心C时，求直线l的方程；
(2)当弦AB被点P平分时，写出直线l的方程；
(3) 当直线l的倾斜角为45º时，求弦AB的长.
粤公网安备 44130202000953号