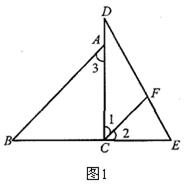
【改编】将一副三角板拼成如图1所示的图形，过点C作CF平分∠DCE交DE于点F．
（1）试确定CF与AB的位置关系并说明理由．
（2）∠DFC= °．
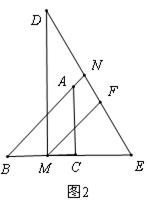
（3）若如图2、图3所示放置两个三角板时，设BA与DE交于点N，试确定∠DNB的大小是否发生变化，若不变，求出∠DNB的度数，若变化，说明理由．
【改编】将一副三角板拼成如图1所示的图形，过点C作CF平分∠DCE交DE于点F．
（1）试确定CF与AB的位置关系并说明理由．
（2）∠DFC= °．
（3）若如图2、图3所示放置两个三角板时，设BA与DE交于点N，试确定∠DNB的大小是否发生变化，若不变，求出∠DNB的度数，若变化，说明理由．
中，
，
，
的垂直平分线
交
，交
，
.求
的长.
（2）
（4）
即
。
＝；
＝。
－ab的值．
粤公网安备 44130202000953号