为了解教学情况,某校抽取了部分初三年级学生期末数学考试成绩,将所得分数整理后,画出频率分布直方图(分数取整数,满分120分),如图所示,图中从左到右各小组的小长方形面积之比是5:16:13:9:7,第一小组的频数为10.
请根据以上信息,回答下列问题:
(1)填空:第一小组的频率为________ ;
(2)填空:在这个问题中,样本的容量是___________ ;
(3)若分数在81分以上(含81分)为合格,试估计该校初三学生数学成绩的合格率是多少?(写出计算过程,并作答)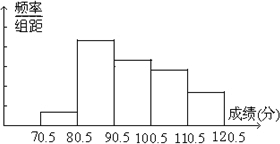
为了解教学情况,某校抽取了部分初三年级学生期末数学考试成绩,将所得分数整理后,画出频率分布直方图(分数取整数,满分120分),如图所示,图中从左到右各小组的小长方形面积之比是5:16:13:9:7,第一小组的频数为10.
请根据以上信息,回答下列问题:
(1)填空:第一小组的频率为________ ;
(2)填空:在这个问题中,样本的容量是___________ ;
(3)若分数在81分以上(含81分)为合格,试估计该校初三学生数学成绩的合格率是多少?(写出计算过程,并作答)