（本小题满分12分）设函数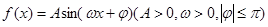
的图象的最高点D的坐标为（2,
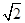），由最高点运动到相邻的最低点F时，曲线与x轴相交于点E（6,0）.
（1）求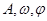
的值；
（2）求函数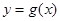
，使其图象与
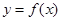图象关于直线
对称.
相关试题
个人坐在一排
个座位上,问(1)空位不相邻的坐法有多少种?
个空位只有
个相邻的坐法有多少种?
个相邻的坐法有多少种?
，被甲或乙解出的概率为
，（1）求该题被乙独立解出的概率；
的数学期望和方差
中，
，点
是
的中点.
；（2）
平面
.
是公差为正数的等差数列，若
,
。
，
，求
。相关知识点
推荐套卷
（本小题满分12分）设函数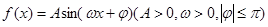的图象的最高点D的坐标为（2,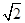），由最高点运动到相邻的最低点F时，曲线与x轴相交于点E（6,0）.
（1）求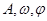的值；
（2）求函数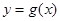，使其图象与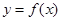图象关于直线对称.
粤公网安备 44130202000953号