（本小题满分12分）若函数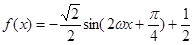
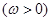的图象与直线
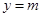相切，
并且相邻两个切点的距离为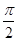
．
（1）求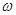
，
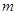的值；
（2）将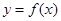
的图象向右平移
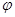个单位后，所得的图象
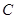对应的函数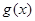
恰好是偶函数，求最
小正数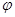，并求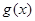的单调递增区间。
，且
，求
的解析式；
，试问：是否存在实数
，使
在
内为减函数，且在（－1，0）内是增函数．
；
；
（
且
）；
（
是可导函数）
；（2）
；（2）
；
；（4）
。相关知识点
推荐套卷
（本小题满分12分）若函数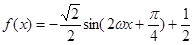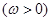的图象与直线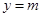相切，
并且相邻两个切点的距离为．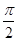
（1）求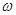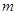，的值；
（2）将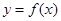的图象向右平移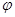个单位后，所得的图象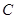对应的函数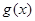 恰好是偶函数，求最
小正数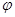，并求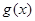的单调递增区间。
粤公网安备 44130202000953号