设函数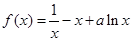 (
(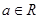 )(
)( 是一个无理数)
是一个无理数)
(1)若函数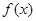 在定义域上不是单调函数,求a的取值范围;
在定义域上不是单调函数,求a的取值范围;
(2)设函数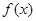 的两个极值点为
的两个极值点为 和
和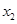 ,记过点
,记过点 、
、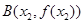 的直线
的直线
的斜率为k,是否存在a, 使得 ?若存在,求出a的取值集合;若不存在,请说明理由.
?若存在,求出a的取值集合;若不存在,请说明理由.
推荐套卷
设函数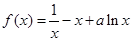 (
(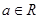 )(
)( 是一个无理数)
是一个无理数)
(1)若函数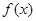 在定义域上不是单调函数,求a的取值范围;
在定义域上不是单调函数,求a的取值范围;
(2)设函数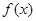 的两个极值点为
的两个极值点为 和
和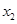 ,记过点
,记过点 、
、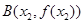 的直线
的直线
的斜率为k,是否存在a, 使得 ?若存在,求出a的取值集合;若不存在,请说明理由.
?若存在,求出a的取值集合;若不存在,请说明理由.