为了研究玉米品种对产量的影响,某农科院对一块试验田种植的一批玉米共10000株的生长情况进行研究,现采用分层抽样方法抽取50株作为样本,统计结果如下:
|
高茎
|
矮茎
|
合计
|
圆粒
|
11
|
19
|
30
|
皱粒
|
13
|
7
|
20
|
合计
|
24
|
26
|
50
|
(1) 现采用分层抽样的方法,从该样本所含的圆粒玉米中取出6株玉米,再从这6株玉米中随机选出2株,求这2株之中既有高茎玉米又有矮茎玉米的概率;
(2) 根据对玉米生长情况作出的统计,是否能在犯错误的概率不超过0.050的前提下认为玉米的圆粒与玉米的高茎有关?(下面的临界值表和公式可供参考:
P(K2≥k)
|
0.15
|
0.10
|
0.05
|
0.025
|
0.010
|
0.005
|
0.001
|
k
|
2.072
|
2.706
|
3.841
|
5.024
|
6.635
|
7.879
|
10.828
|
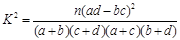 ,其中
,其中 )
)