如图,已知椭圆 (a>b>0)过点(1,
(a>b>0)过点(1,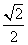 ),离心率为
),离心率为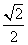 ,左、右焦点分别为F1、F2.点P为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.
,左、右焦点分别为F1、F2.点P为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.
(1)求椭圆的标准方程.
(2)设直线PF1、PF2的斜率分别为k1、k2.
(ⅰ)证明: =2.
=2.
(ⅱ)问直线l上是否存在点P,使得直线OA、OB、OC、OD的斜率kOA、kOB、kOC、kOD满足kOA+kOB+kOC+kOD=0?若存在,求出所有满足条件的点P的坐标;若不存在,说明理由.
推荐套卷
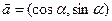 ,
, 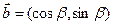 ,
, 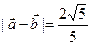 .
.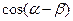 的值;
的值;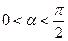 ,
, 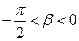 , 且
, 且 , 求
, 求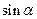 .
. ,函数
,函数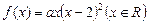 .
.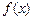 有极大值32,求实数
有极大值32,求实数 的值;(Ⅱ)若对
的值;(Ⅱ)若对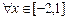 ,不等式
,不等式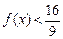 恒成立,求实数
恒成立,求实数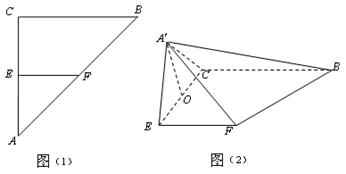
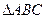 是等腰直角三角形,
是等腰直角三角形, ,
,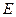 、
、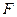 分别为
分别为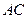 、
、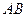 的中点,将
的中点,将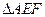 沿
沿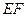 折起,使
折起,使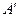 在平面
在平面 上的射影
上的射影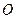 恰为
恰为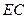 的中点,得到图(2).
的中点,得到图(2).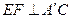 ;
; 的体积.
的体积. ,不等式
,不等式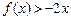 的解集为
的解集为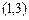 .(Ⅰ)若方程
.(Ⅰ)若方程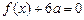 有两个相等的实根,求
有两个相等的实根,求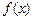 的解析式;(Ⅱ)若
的解析式;(Ⅱ)若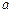 的取值范围.
的取值范围. 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,已知
,已知 ,
,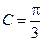 .
.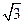 ,求
,求 ;
; ,求
,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号