(理科)已知椭圆C: 的离心率为
的离心率为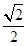 ,且经过点
,且经过点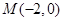 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设直线l: 与椭圆C相交于
与椭圆C相交于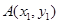 ,
, 两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且
两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且 .求证:直线
.求证:直线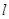 过定点.
过定点.
推荐套卷
(理科)已知椭圆C: 的离心率为
的离心率为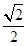 ,且经过点
,且经过点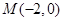 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设直线l: 与椭圆C相交于
与椭圆C相交于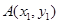 ,
, 两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且
两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且 .求证:直线
.求证:直线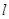 过定点.
过定点.