(理科)已知顶点在坐标原点,焦点在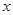 轴正半轴的抛物线上有一点
轴正半轴的抛物线上有一点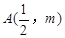 ,
,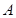 点到抛物线焦点的距离为1.
点到抛物线焦点的距离为1.
(1)求该抛物线的方程;
(2)设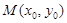 为抛物线上的一个定点,过
为抛物线上的一个定点,过 作抛物线的两条互相垂直的弦
作抛物线的两条互相垂直的弦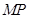 ,
,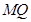 ,求证:
,求证: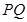 恒过定点
恒过定点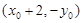 .
.
(3)直线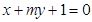 与抛物线交于
与抛物线交于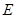 ,
,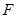 两点,在抛物线上是否存在点
两点,在抛物线上是否存在点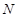 ,使得△
,使得△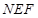 为以
为以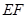 为斜边的直角三角形.
为斜边的直角三角形.
推荐套卷
(理科)已知顶点在坐标原点,焦点在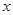 轴正半轴的抛物线上有一点
轴正半轴的抛物线上有一点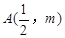 ,
,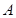 点到抛物线焦点的距离为1.
点到抛物线焦点的距离为1.
(1)求该抛物线的方程;
(2)设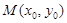 为抛物线上的一个定点,过
为抛物线上的一个定点,过 作抛物线的两条互相垂直的弦
作抛物线的两条互相垂直的弦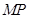 ,
,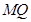 ,求证:
,求证: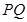 恒过定点
恒过定点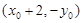 .
.
(3)直线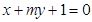 与抛物线交于
与抛物线交于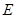 ,
,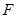 两点,在抛物线上是否存在点
两点,在抛物线上是否存在点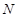 ,使得△
,使得△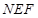 为以
为以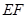 为斜边的直角三角形.
为斜边的直角三角形.