(理科)如图,已知⊙ :
: 及点
及点
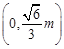 ,在 ⊙
,在 ⊙ 上任取一点
上任取一点 ′,连
′,连
 ′,并作
′,并作
 ′的中垂线l,设l与
′的中垂线l,设l与
 ′交于点P, 若点
′交于点P, 若点 ′取遍⊙
′取遍⊙ 上的点.
上的点.

(1)求点P的轨迹C的方程;
(2)设直线 与轨迹C相交于A、B两个不同的点,与x轴相交于点D.若
与轨迹C相交于A、B两个不同的点,与x轴相交于点D.若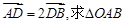 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
推荐套卷
(理科)如图,已知⊙ :
: 及点
及点
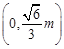 ,在 ⊙
,在 ⊙ 上任取一点
上任取一点 ′,连
′,连
 ′,并作
′,并作
 ′的中垂线l,设l与
′的中垂线l,设l与
 ′交于点P, 若点
′交于点P, 若点 ′取遍⊙
′取遍⊙ 上的点.
上的点.

(1)求点P的轨迹C的方程;
(2)设直线 与轨迹C相交于A、B两个不同的点,与x轴相交于点D.若
与轨迹C相交于A、B两个不同的点,与x轴相交于点D.若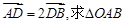 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.