已知关于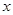 的一元二次方程
的一元二次方程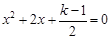 有实数根,
有实数根,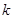 为正整数.
为正整数.
(1)求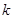 的值;
的值;
(2)当此方程有两个非零的整数根时,将关于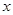 的二次函数
的二次函数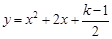 的图象向下平移9个单位,求平移后的图象的表达式;
的图象向下平移9个单位,求平移后的图象的表达式;
(3)在(2)的条件下,平移后的二次函数的图象与x轴交于点A,B(点A在点B左侧),直线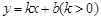 过点B,且与抛物线的另一个交点为C,直线BC上方的抛物线与线段BC组成新的图象,当此新图象的最小值大于-5时,求k的取值范围.
过点B,且与抛物线的另一个交点为C,直线BC上方的抛物线与线段BC组成新的图象,当此新图象的最小值大于-5时,求k的取值范围.
已知关于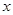 的一元二次方程
的一元二次方程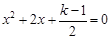 有实数根,
有实数根,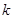 为正整数.
为正整数.
(1)求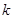 的值;
的值;
(2)当此方程有两个非零的整数根时,将关于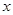 的二次函数
的二次函数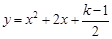 的图象向下平移9个单位,求平移后的图象的表达式;
的图象向下平移9个单位,求平移后的图象的表达式;
(3)在(2)的条件下,平移后的二次函数的图象与x轴交于点A,B(点A在点B左侧),直线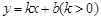 过点B,且与抛物线的另一个交点为C,直线BC上方的抛物线与线段BC组成新的图象,当此新图象的最小值大于-5时,求k的取值范围.
过点B,且与抛物线的另一个交点为C,直线BC上方的抛物线与线段BC组成新的图象,当此新图象的最小值大于-5时,求k的取值范围.