如图,已知二次函数y= x2-2x+3的图象的顶点为A,且与y轴交于点C.
x2-2x+3的图象的顶点为A,且与y轴交于点C.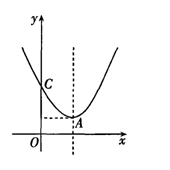
(1)求点A与点C的坐标;
(2)若将此函数的图象沿x轴向右平移1个单位,再沿y轴向下平移3个单位,请直接写出平移后图象所对应的函数关系式及点C的对应点的坐标;
(3)若A(m,y1),B(m+1,y2)两点都在此函数的图象上,试比较y1与y2的大小.
如图,已知二次函数y= x2-2x+3的图象的顶点为A,且与y轴交于点C.
x2-2x+3的图象的顶点为A,且与y轴交于点C.
(1)求点A与点C的坐标;
(2)若将此函数的图象沿x轴向右平移1个单位,再沿y轴向下平移3个单位,请直接写出平移后图象所对应的函数关系式及点C的对应点的坐标;
(3)若A(m,y1),B(m+1,y2)两点都在此函数的图象上,试比较y1与y2的大小.