(本小题满分16分)如图,在平面直角坐标系 xOy 中,A,B 是圆 O: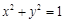 与 x 轴的两个交点(点 B 在点 A右侧),点 Q(-2,0), x 轴上方的动点 P 使直线 PA,PQ,PB 的斜率存在且依次成等差数列.
与 x 轴的两个交点(点 B 在点 A右侧),点 Q(-2,0), x 轴上方的动点 P 使直线 PA,PQ,PB 的斜率存在且依次成等差数列.
(Ⅰ)求证:动点 P 的横坐标为定值;
(Ⅱ)设直线 PA,PB 与圆 O 的另一个交点分别为 S,T,求证:点 Q,S,T 三点共线.
相关知识点
推荐套卷
(本小题满分16分)如图,在平面直角坐标系 xOy 中,A,B 是圆 O: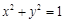 与 x 轴的两个交点(点 B 在点 A右侧),点 Q(-2,0), x 轴上方的动点 P 使直线 PA,PQ,PB 的斜率存在且依次成等差数列.
与 x 轴的两个交点(点 B 在点 A右侧),点 Q(-2,0), x 轴上方的动点 P 使直线 PA,PQ,PB 的斜率存在且依次成等差数列.
(Ⅰ)求证:动点 P 的横坐标为定值;
(Ⅱ)设直线 PA,PB 与圆 O 的另一个交点分别为 S,T,求证:点 Q,S,T 三点共线.