（本小题满分12分）已知广东省某校高三（1）班有
名学生，从中按系统抽样抽取
名学生．
（Ⅰ）若第
组抽出的号码为
，写出所有被抽出学生的号码；
（Ⅱ）分别统计这名学生的某高校自主招生考试成绩（满分：
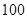分），获得成绩数据的茎叶图如图所示，现从这名学生中随机抽取两名成绩超过平均分的学生，求成绩为
分的学生被抽取到的概率．
的解集是
，求不等式
的解集
中，
求
的值
（2）
,
.
在
上为单调函数,求m的取值范围；
,若在
上至少存在一个
，使得
成立，求
的取值范围.
（
）过点
（0，2），离心率
.
（2，0）的直线
与椭圆相交于
两点，且
为锐角（其中
为坐标原点),求直线推荐套卷
（本小题满分12分）已知广东省某校高三（1）班有名学生，从中按系统抽样抽取名学生．
（Ⅰ）若第组抽出的号码为，写出所有被抽出学生的号码；
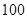（Ⅱ）分别统计这名学生的某高校自主招生考试成绩（满分：分），获得成绩数据的茎叶图如图所示，现从这名学生中随机抽取两名成绩超过平均分的学生，求成绩为分的学生被抽取到的概率．
粤公网安备 44130202000953号