（本小题满分14分）已知圆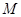
经过第一象限，与
轴相切于点
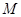，且圆上的点到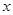
轴的最大距离为2，过点
作直线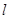
．
（1）求圆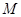的标准方程；
（2）当直线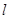与圆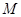相切时，求直线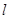的方程；
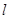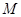（3）当直线与圆相交于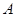
、
两点，且满足向量
，
时，求
的取值范围．
满足
，求数列
满足
，
，求数列
，sinα+cosβ的取值范围是D，x∈D，求函数y=
的最小值，并求取得最小值时x的值.
+x)=
，(
＜x＜
)，求
的值相关知识点
推荐套卷
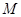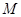（本小题满分14分）已知圆经过第一象限，与轴相切于点，且圆上的点到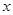轴的最大距离为2，过点作直线．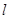
（1）求圆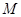的标准方程；
（2）当直线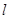与圆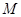相切时，求直线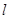的方程；
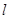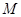（3）当直线与圆相交于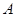、两点，且满足向量，时，求的取值范围．
粤公网安备 44130202000953号