(本小题满分14分)设函数
 .
.
(1)当函数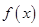 在定义域内为增函数时,求
在定义域内为增函数时,求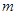 的取值范围;
的取值范围;
(2)设 是曲线
是曲线 上的两个不同点,且曲线在
上的两个不同点,且曲线在 两点处的切线均与
两点处的切线均与 轴平行,直线
轴平行,直线 的斜率为
的斜率为 ,是否存在
,是否存在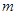 使得
使得 ,若存在,请求出
,若存在,请求出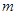 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
推荐套卷
(本小题满分14分)设函数
 .
.
(1)当函数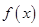 在定义域内为增函数时,求
在定义域内为增函数时,求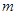 的取值范围;
的取值范围;
(2)设 是曲线
是曲线 上的两个不同点,且曲线在
上的两个不同点,且曲线在 两点处的切线均与
两点处的切线均与 轴平行,直线
轴平行,直线 的斜率为
的斜率为 ,是否存在
,是否存在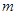 使得
使得 ,若存在,请求出
,若存在,请求出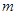 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.