已知,如图,一次函数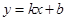 与x轴、y轴分别交于点A和点B,A点坐标为(3,0),∠OAB=45°.
与x轴、y轴分别交于点A和点B,A点坐标为(3,0),∠OAB=45°.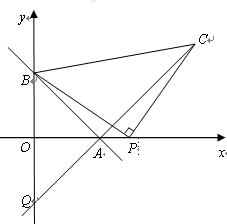
(1)求一次函数的表达式;
(2)点P是x轴正半轴上一点,以P为直角顶点,BP为腰在第一象限内作等腰Rt△BPC,连接CA并延长交y轴于点Q.
①若点P的坐标为(4,0),求点C的坐标,并求出直线AC的函数表达式;
②当P点在x轴正半轴运动时,Q点的位置是否发现变化?若不变,请求出它的坐标;如果变化,请求出它的变化范围.
相关知识点
推荐套卷
已知,如图,一次函数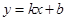 与x轴、y轴分别交于点A和点B,A点坐标为(3,0),∠OAB=45°.
与x轴、y轴分别交于点A和点B,A点坐标为(3,0),∠OAB=45°.
(1)求一次函数的表达式;
(2)点P是x轴正半轴上一点,以P为直角顶点,BP为腰在第一象限内作等腰Rt△BPC,连接CA并延长交y轴于点Q.
①若点P的坐标为(4,0),求点C的坐标,并求出直线AC的函数表达式;
②当P点在x轴正半轴运动时,Q点的位置是否发现变化?若不变,请求出它的坐标;如果变化,请求出它的变化范围.