(本小题满分16分)已知数列 、
、 满足
满足 ,
, ,其中
,其中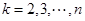 ,则称
,则称 为
为 的“生成数列”.
的“生成数列”.
(1)若数列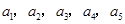 的“生成数列”是
的“生成数列”是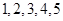 ,求
,求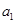 ;
;
(2)若 为偶数,且
为偶数,且 的“生成数列”是
的“生成数列”是 ,证明:
,证明: 的“生成数列”是
的“生成数列”是 ;
;
(3)若 为奇数,且
为奇数,且 的“生成数列”是
的“生成数列”是 ,
, 的“生成数列”是
的“生成数列”是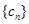 , ,依次将数列
, ,依次将数列 ,
, ,
,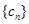 , 的第
, 的第 项取出,构成数列
项取出,构成数列 .探究:数列
.探究:数列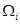 是否为等比数列,并说明理由.
是否为等比数列,并说明理由.
推荐套卷
(本小题满分16分)已知数列 、
、 满足
满足 ,
, ,其中
,其中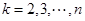 ,则称
,则称 为
为 的“生成数列”.
的“生成数列”.
(1)若数列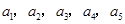 的“生成数列”是
的“生成数列”是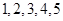 ,求
,求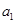 ;
;
(2)若 为偶数,且
为偶数,且 的“生成数列”是
的“生成数列”是 ,证明:
,证明: 的“生成数列”是
的“生成数列”是 ;
;
(3)若 为奇数,且
为奇数,且 的“生成数列”是
的“生成数列”是 ,
, 的“生成数列”是
的“生成数列”是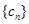 , ,依次将数列
, ,依次将数列 ,
, ,
,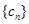 , 的第
, 的第 项取出,构成数列
项取出,构成数列 .探究:数列
.探究:数列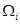 是否为等比数列,并说明理由.
是否为等比数列,并说明理由.