如图: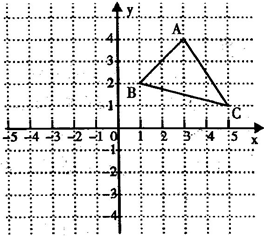
①写出A、B、C三点的坐标.A ( ) B( ) C( )
②若△ABC各顶点的横坐标不变,纵坐标都乘以-1,请你在同一坐标系中描出对应的点 A′、B′、C′,并依次连接这三个点,所得的△A′B′C′与原△ABC有怎样的位置关系?
③在②的基础上,纵坐标都不变,横坐标都乘以-1在同一坐标系中描出对应的点A″、B″、C″,并依次连接这三个点,所得的△A″B″C″与原△ABC有怎样的位置关系?
相关知识点
推荐套卷
 ,其中
,其中


 时,求OD的长;
时,求OD的长;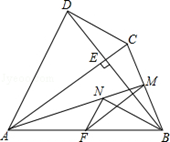
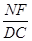 的值.
的值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号