(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为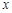 (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为 (m2).
(m2).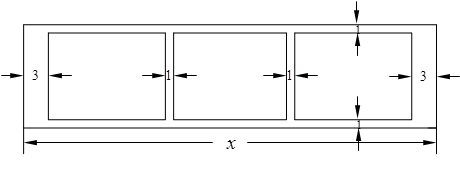
(1)求 关于
关于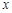 的函数关系式;
的函数关系式;
(2)求 的最大值.
的最大值.
推荐套卷
(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为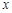 (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为 (m2).
(m2).
(1)求 关于
关于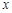 的函数关系式;
的函数关系式;
(2)求 的最大值.
的最大值.